If we insert this expression in a Maxwell-Boltzmann distribution. Ii the fraction of molecules with most probable kinetic energy increases at higher temperatures.
To represent the probability for a given energy it must be normalized to a probability of 1.
Boltzmann distribution of kinetic energy. This microscopic kinetic energy is often called thermal energy and this expression is useful in defining the kinetic temperature. Note that the average kinetic energy for molecules is not the same as the average energy for purely random energies under the Boltzmann distribution which is E avg kT. If you consider all velocities to be equally probable then all velocities within a range v to vΔv can be.
The Boltzmann distribution describes the distribution of energy among classical distinguishable particles. It can be used to evaluate the average energy per particle in the circumstance where there is no energy-dependent density of states to skew the distribution. To represent the probability for a given energy it must be normalized to a probability of 1.
So I was trying to arrange the expression of a Maxwell-Boltzmann velocity vector distribution into a kinetic energy distribution. Since we know that E 1 2 m v 2 we can rearrange this expression to give v 2 2 E m. If we insert this expression in a Maxwell-Boltzmann distribution.
F v m 2 π K B T. The Maxwell law of molecular velocities f v is a particular case of the Boltzmann distribution of energy levels if one equals to ε the kinetic energy Ec. From this point of view the velocity distribution function f v becomes 96fυ m 2πkTe mυ2 2kT.
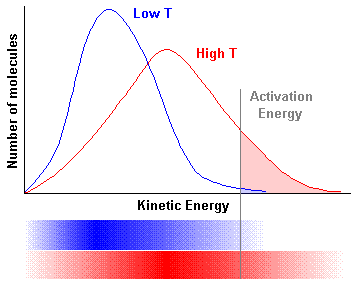
The kinetic energy distribution of molecules at a particular temperature can be calculated using equations derived by James Clerk Maxwell and Ludwig Boltzmann in the nineteenth century 3. For this reason the kinetic energy distribution is referred to as the Maxwell-Boltzmann distribution. The answer is the option i iii Maxwell Boltzmann distribution of kinetic energy can be described by a graph plotted with fraction of molecules on y-axis versus kinetic energy on x-axis.
Most probable kinetic energy is the kinetic energy of maximum fraction of molecule. According to Maxwell Boltzmann distributon of energy _____. I the fraction of molecules with most probable kinetic energy decreases at higher temperatures.
Ii the fraction of molecules with most probable kinetic energy increases at higher temperatures. Iii most probable kinetic energy increases at higher temperatures. Need help with chemistry.
Analysis of Agglomeration Kinetics of Magnetic Nanoparticles With Boltzmann Distribution of Energy Barrier. Department of Chemistry Chungnam National University Daejeon 34134 Korea. Search for more papers by this author.
The Maxwell-Boltzmann equation which forms the basis of the kinetic theory of gases defines the distribution of speeds for a gas at a certain temperature. From this distribution function the most probable speed the average speed and the root-mean-square speed can be derived. This general distribution known as the MaxwellBoltzmann distribution either expressed in terms of velocity Maxwell or energy Bolzmann is referred to as an increasing series of small intervals composed of molecules characterized by the same kinetic energy Ec.
Maxwell and Boltzmann discovered that this distribution may be described by plotting the fraction of molecules in a container with a given kinetic energy vs kinetic energy. Notice that the plot is not symmetrical so the most probable speed is not the same as the average speed. Derive the average kinetic energy of a molecular system at temperature T with a molar mass M starting from the Boltzmann distribution of speed.
Derive the average kinetic energy of a molecular system at temperature T with a molar mass M starting from the Boltzmann distribution of speed. Maxwell-Boltzmann Distribution Scottish physicist James Clerk Maxwell developed his kinetic theory of gases in 1859. Maxwell determined the distribution of velocities among the molecules of a gas.
Maxwells finding was later generalized in 1871 by a German physicist Ludwig Boltzmann to express the distribution of energies among the molecules.
