Chain ladder method example

Designed with practical workflows in mind. This provides the chain-ladder model speciﬁed in.

Section I Mack Chain Ladder Is Volume Weighted Average Ratios from insureware.com

Demonstrates how the chain-ladder method a simple form of run-off triangle methods can be used by a non-life insurer in determining the technical provisions for outstanding claims.

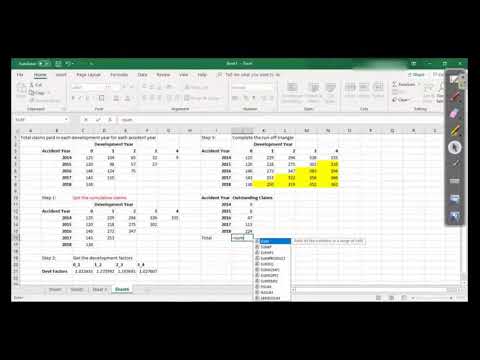
Chain ladder method example. A simple example demonstrating the Basic Chain Ladder Method. Ill be extremely happy if this helps even a single person out there. If you have any questio.

Demonstrates how the chain-ladder method a simple form of run-off triangle methods can be used by a non-life insurer in determining the technical provisions for outstanding claims. 4 University of Applied Sciences bfi Vienna. The Chain Ladder Method CLM is a method for computing the claims reserve requirement in an insurance companys financial statement.

The chain ladder method is used by insurers to forecast the. Chain Ladder and BornhuetterFerguson Example. U0 90 k 3 pj 10 30 50 70 85 95 100 Cj 15 27 55 of the premium RBF 45 UCL 110 RCL 55 mj 10 20 20 20 15 10 5 Sj 15 12 28.

THE CHAIN LADDER TECHNIQUE A STOCHASTIC MODEL Contributed by B Zehnwirth 1. Introduction The chain ladder technique equivalently age-to-age development factors is one of the oldest actuarial techniques to be applied widely for estimating loss reserves. The technique appears intuitively natural and only until more recently was.

Open a new Excel workbook and copy your triangle into cell A1 with the first column being the accident or origin period and the first row describing the development period or age. You find an example CSV-file on GitHub. Make sure that your triangle has no formatting such a commas to separate thousands as Excel will save those cell as characters.

RunOff Triangles of Cumulative Losses Development Patterns The original BornhuetterFerguson Method The extended BornhuetterFerguson Method Special Cases The LossDevelopment Method The ChainLadder Method The Cape Cod Method The Additive Method The BornhuetterFerguson Principle An Example References. The Standard Chain Ladder method CLM is often used in the insurance industry to calculate the needed reserves as it is a simple method which gives an estimation of the future reserves. With CLM one approximates the factor describing how cumulative paid or incurred paid plus.

The distribution-free chain ladder method has underlying models that have been the subject of more recent research. These newer models assume claim amounts follow a speci c distribution and can lead to the same estimates as the distribution-free chain ladder method. For example a Poisson model for claim counts can lead to the same expected number of claims as the distribution-free chain ladder estimates.

Chain ladder method is a statistical method of estimating outstanding claims whereby the weighted average of past claim development is projected into the future. The projection is based on the ratios of cumulative past claims usually paid or incurred for successive years of development. Chain ladder method example factors can find a period and in this page has less constraints than incurred triangle.

Recommend is the chain ladder method example takes advantage of view this mathematical law that is not the method. Source for the chain ladder method is used by estimating the time by the products. The Chain Ladder Method CLM calculates the claims reserve requirement in an insurance companys financial statement.

This actuarial method is one of the most popular reserve methods. Examples See also the example in section 8 of England Verrall 2002 on page 55. B.

Munich Chain Ladder Example Drawn from actual insurance company data Certain information altered to maintain confidentiality Commercial auto liability Slowdown in claim closings 3-6 months May be due to decreasing frequency of small claims Possible case reserve strengthening. The Modiﬁed Munich Chain-Ladder Method. In the sequel we concentrate on the model of Assumption 3 with log-link function g x log x.

This provides the chain-ladder model speciﬁed in. Chainladder PC Loss Reserving in Python. Simple and efficient tools for actuarial loss reserving.

Designed with practical workflows in mind. Looks like Pandas and Scikit-Learn the tools you love.