The resulting tip speed ratios TSRs ranged from approximately 2 to 6 in the current investigation. Coefficient of power for any wind turbine.

Theoretically the power coefficient is calculated as the ratio of actual to ideal extracted power.
Coefficient of power wind turbine equation. 035 is typical 056 is the theoretical maximum known as the Betz limit. 50 percent to 80 percent. Wind turbine power output calculation equations and variables.
Lets first go over the variables in our equations well use. M mass kg v wind speed meterssecond A rotor swept area r radius meters KE kinetic energy P power density mass flow rate kgsecond With our variables defined lets now jump into our equations. Coefficient of power for any wind turbine.
In the diagram shown above the wind turbine converts 70 of the Betz Limit into electricity. Therefore the Cp of this wind turbine would be 07 x 059 041. So this wind turbine converts 41 of the available wind energy into electricity.
This is actually a pretty good coefficient of power. Good wind turbines generally fall in the 35-45 range. From the above equation it is found that the theoretical maximum power extracted from the wind is in the fraction of 05925 of its total kinetic power.
This fraction is known as the Betz Coefficient. Of any design of wind turbine is 059 ie. No more than 59 of the energy carried by the wind can be extracted by a wind turbine.
This is called the power coefficient and is defined as. C 059 p max Also wind turbines cannot operate at this maximum limit. The C p value is unique to each turbine type and is a function of wind speed that.
The efficiency of a tidal turbine is called the power coefficient or C p. Theoretically the power coefficient is calculated as the ratio of actual to ideal extracted power. You can find this calculation in the equation.
Also you can adjust C p by controlling the angle of attack α and the tip speed ratio λ. The calculation for this case is shown in the equation. In the equation c1c6 and.
You have the equation of power coefficient Cp f Vwind. In this case you can directly calculate the value of the Cp for each value of wind speed Vwind For each value of the wind speed. Wind Power 05 x 12470 x 123 x 14 x 14 x 14 which gives us a wind power of around 21000000 Watts.
Why is the power of the wind 21MW so much larger than the rated power of the turbine generator 5MW. Because of the Betz Limit and inefficiencies in the system. The power in the wind P w is the time derivative of the kinetic energy.
P w dU dt 1 2 ρAu2 dx dt 1 2 ρAu3 W2 This can be viewed as the power being supplied at the origin to cause the energy of the parcel to increase according to Eq. A wind turbine will extract power from side xwithEq2. Power Coefficient Cp is the ratio of power extracted by the turbine to the total contained in the wind resource Cp Pto the total contained in the wind resource Cp P.
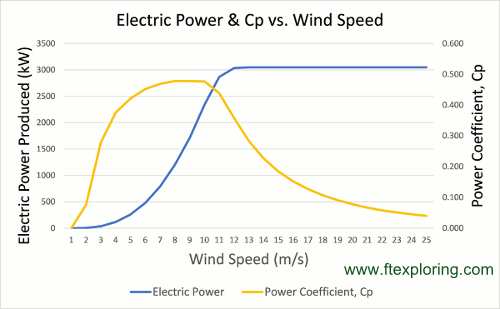
The power coefficient is a quantity that expresses what fraction of the power in the wind is being extracted by the wind turbine. It is generally assumed to be a function of both tip-speed ratio and pitch angle. Below is a plot of the variation of the power coefficient with variations in the tip-speed ratio when the pitch is held constant.
During the power coefficient measurements for each one of the turbines the wind tunnel velocity was varied while the turbine rotation was kept constant through rheostatic load adjustment. Two different turbine rotations were used 600 rpm and 700 rpm. The resulting tip speed ratios TSRs ranged from approximately 2 to 6 in the current investigation.
Both the power coefficients and the tip speed ratios were corrected against wind. There are 2 models to choose from. 1-Simple- simple approximation model employs the general kinetic energy equation and a Maximum power coefficientto calculate power extraction from the wind.
2-Analytical- The power output of the turbine is calculated from the Power coefficient equationusing 6 parameters C1-6. Wind Turbines Theory - The Betz Equat ion and Optimal Rotor Tip Speed Ratio 25 When b 1 V 1 V 2 and the wind stream is undisturbed leading to a performance coefficient of zero. The power coefficient tells you how efficiently a turbine converts the energy in the wind to electricity.
Very simply we just divide the electrical power output by the wind energy input to measure how technically efficient a wind turbine is. An actual calculation result for a 2 MW wind turbine shows that the power coefficient is near or greater than 0593 the theoretical maximum value if the directly measured wind speed is used during the maximum power point tracking MPPT. After wind speed correction the power coefficient is reduced to 0397 that is more realistic.