Explain single channel queuing model

Single-Channel Queuing Model with Poisson Arrivals and Exponential Service-Times Model B MMS. Total system time of all customers is also given by the total area under the number-in-system function Lt.

Single-Channel Queuing Model with Poisson Arrivals and Exponential Service-Times Model B MMS.

Explain single channel queuing model. Let n be the number of units in the system and P n t be the probability of n units in the system at time t. The derivation of expressions is done in three steps. Find P n t in terms of λ and μ.

Using this expression find the expected number of units in the system in terms of λ and μ. Up to 5 cash back The single channel queuing model referred above is the most simple model which is based on the above mentioned assumptions. However in reality there are several limitations of this model in its applications.

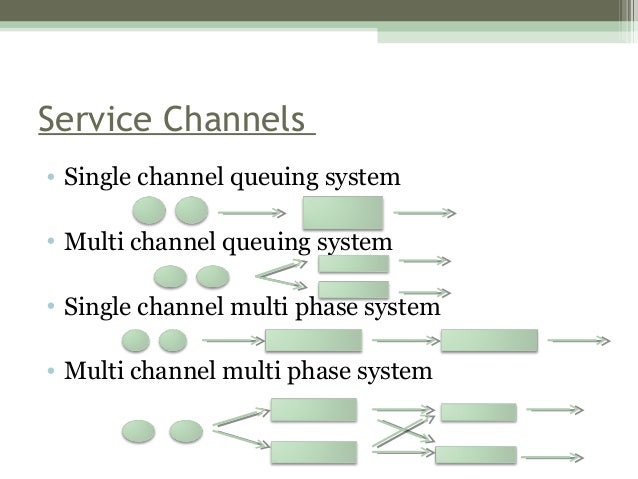
One obvious limitation is the possibility that the waiting space may in fact be limited. Another possibility is that arrival rate is state dependent. 211 Single Channel Queues If the organization has provided single facility to serve the customers only one unit can be served at a time hence arriving customers form a queue near the facility.

The next element is drawn into service only when the service of the previous customer is over. 5 rows The simplest type of waiting line structure is the single-channel single-phase. It is a queuing model where the arrivals follow a Poisson process service times are exponentially distributed and there is only one server.

In other words it is a system with Poisson input exponential waiting time and Poisson output with single channel. This holds for most queueing systems Sketch of derivation for a single server FIFO queueing model. Total system time of all customers is also given by the total area under the number-in-system function Lt.

𝑖1 𝑁 𝑊𝑖 0 𝑡𝑑𝑡 Therefore 1 0 𝑡𝑑𝑡1 𝑁 𝑁 𝑖1 𝑁𝑊 𝑖 𝑁 1 𝑁 𝑖1. Single Server Queuing System MM1 Poisson arrivals Arrival population is unlimited Exponential service times All arrivals wait to be served λ is constant μ λ average service rate average arrival rate 19. Operating Characteristics for MM1 Queue 1.

Average server utilization ρ λ μ 2. Multiple-Server Queuing Model with Poisson Arrivals and Exponential Service Times The model adopted in this paper is multiple channel queuing system in which two or more servers or channels are available to handle arriving customers. Let still assume that customers waiting service form one single line and then proceed to the.

Measuring the Queues Performance QUEUING COSTS THE VARIETY OF QUEUING MODELS Model A MM1. Single-Channel Queuing Model with Poisson Arrivals and Exponential Service-Times Model B MMS. Multiple-Channel Queuing Model Model C MD1.

Constant Service-Time Model Model D. Limited-Population Model OTHER QUEUING APPROACHES SUMMARY KEY TERMS. The principal difference between multiple- and single-channel queueing-processes is that the former exhibit a greater variety of queue-disciplines.

The possibilities of unusual customer behaviour are more often realized. It is not at all a simple task to formulate mathematical rules to model processes with the more amorphous types of queue-discipline. Systems with one server only are called Single Channel Systems systems with more servers are called Multi Channel Systems.

Output represents the way customers leave the system. Output is mostly ignored by theoretical models but sometimes the customers leaving the server enter the queue again round robin time-sharing systems. Queuing theory is the mathematical study of the delays of waiting in line covering all aspects from arrival time to the number of servers.

This example is a classic first example in digital systems. Namely that of a single server queueing system. Banks typically have a single queue where people line up and several tellers to serve them.

This example demonstrates the organization and approach that will be used for the more complex examples later in the book. Referred to as the MM1 queue. 73 Single Channel Queuing Theory 731.

A Arrival Time Distribution. The simple model assumes that the number of arrivals occurring within a given interval of time t follows a Poisson distribution. Analysis of Single Channel-Multi Phase Queue Model.

Approach to explain variables what will be studied. The purpose of thisprogram was to find out the Queuing System Model of the Office of. A Single-Server Queue Specification Model For a job i.

The arrival time is ai The delay in the queue is di The time that service begins is bi ai di The service time is si The wait in the node is wi di si The departure time is ci ai wi ai bi ci wi.