Fundamental frequency of a string

Similarly the distance from one note to the next a half step higher must be the twelth root of 2. For such a string the fundamental frequency would be Hz.

Frequency of a String.

Fundamental frequency of a string. For such a string the fundamental frequency would be Hz. Any of the highlighted quantities can be calculated by clicking on them. If numerical values are not entered for any quantity it will default to a string of 100 cm length tuned to 440 Hz.

Default values will be entered for any quantity which has a. Determining the Harmonic Frequencies Consider an 80-cm long guitar string that has a fundamental frequency 1st harmonic of 400 Hz. For the first harmonic the wavelength of the wave pattern would be two times the length of the string see table above.

Thus the wavelength is 160 cm or 160 m. 6 rijen The fundamental frequency has one antinode and the 2nd harmonic has two antinodes. The first-pass acyclic DFT shows the fundamental at bin 61 which is 8210 - 067 Hz.

The 2nd pass uses a window length of 53815 8070 so the DFT frequencies include the fundamental period and harmonics of the string. Once the speed of propagation is known the frequency of the sound produced by the string can be calculated. - the shorter the string the higher the frequency of the fundamental - the higher the tension the higher the frequency of the fundamental - the lighter the string the higher the frequency of the fundamental For a string under a tension T with density μ the frequency formula is shown here.

Similarly the distance from one note to the next a half step higher must be the twelth root of 2. Multiply the frequency of the root by the twelth root of 2 and you get the frequency of next higher chromatic note do it again for the next and true to its name do it twelve times and you get the octave back to a factor of two. The lowest or base frequency produced by any particular instrument which we hear the sound at is known as the fundamental frequency.

The fundamental frequency is the supply frequency. It is also called the first harmonic of the instrument. The number of cycles completed by an alternating quantity per second is known as a frequency.

SOLVED A nylon string is stretched between fixed supports 075m apart. Experimental plucking of the string shows that several standing waves can exist on the string. Two such standing waves have frequencies of 225Hz and 300Hz with no other frequencies.

Frequency of a String. Calculates the string frequency from diameter length density and tension of a string or chord. A string oscillates when being drawn eg.

Guitar or struck eg. Piano with a certain fundamental frequency and in theory infinite many harmonic overtones which are integer multiples of the fundamental frequency. A string vibrates with many harmonics that are numerically related to the fundamental frequency.

This combination of fundamental sound from the string resonance and the additional harmonics give the guitar its frequency content and sound. What are the string frequencies dependent on. The frequency of sound a guitar string produces is dependent on a few physical properties.

Frequency of the Fundamental Mode in Terms of Youngs Modulus of Elasticity of the Material of the String. The frequency n of the fundamental mode of transverse vibration of a stretched string is given by Substituting the value of equation 2 and 3 in 1. Click hereto get an answer to your question The fundamental frequency of a string stretched with a weight of 4 kg is 256 Hz.

The weight required to produce its octave is -. Investigation of the variation of fundamental frequency of a stretched string with length Press the Signal ON button. Adjust the frequency of the signal current using the right hand slider at the bottom.

When maximum vibration occurs press the Signal OFF button. Press Get ruler to measure the. This Physics video tutorial explains the concept of standing waves on a string.

It shows you how to calculate the fundamental frequency and any additional h. Investigation of the variation of fundamental frequency of a stretched string with tension. Every object has a natural frequency of vibration.

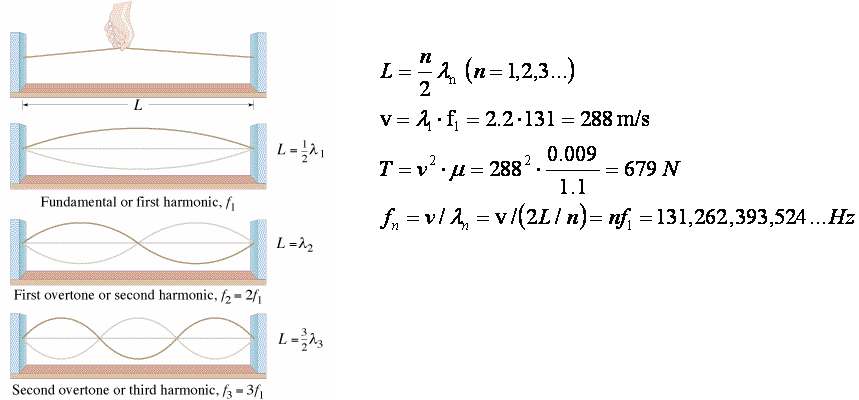
If kinetic energy is applied to an object at a rate that matches its natural frequency resonance occurs and the object vibrates. In this experiment a small current produced by a signal generator causes. If l is the length of the string then l λ 2 or λ 2 l1 Velocity of the wave along the string is v m T 2 where T is the tension and m is the mass per unit length linear density of the string.

Fundamental frequency of vibration of the string is f λ v 2 l v From 1 f 2 l 1 m T From 2. The mode with the lowest frequency f 1 is called the fundamental. Note that the nth mode has frequency n times that of the fundamental.

All of the modes and the sounds they produce are called the harmonics of the string. The frequencies f 2f 3f 4f etc are called the harmonic series.