
One can attain Pareto optimality in this case because the formulation of Model 5 belongs to the category of convex vector optimization which guarantees that any local optimum is a global optimum 5. A bound-constrained multi-objective optimization problem MOP is to find a solution x S R D that minimizes an objective function vector f.
In this post I want to show an alternative approach for solving below multi-objective linear optimization problem.
Multi objective optimization problem. In the single-objective optimization problem the superiority of a solution over other solutions is easily determined by comparing their objective function values In multi-objective optimization problem the goodness of a solution is determined by the dominance Dominance. Definition of Multi-Objective Optimization Problem MOP. The MOP is defined as.
R n is the feasible set and f. R p is a vector valued objective function. Multiobjective optimization involves minimizing or maximizing multiple objective functions subject to a set of constraints.
Example problems include analyzing design tradeoffs selecting optimal product or process designs or any other application where you need an optimal solution with tradeoffs between two or more conflicting objectives. Problems that have more than one objective is referred to as multi-objective optimization MOO. This type of problem is found in everyday life such as mathematics engineering social studies economics agriculture aviation automotive and many others.
The MOO application in the economic field Mardle Pascoe Tamiz 1998. A bound-constrained multi-objective optimization problem MOP is to find a solution x S R D that minimizes an objective function vector f. S R M.
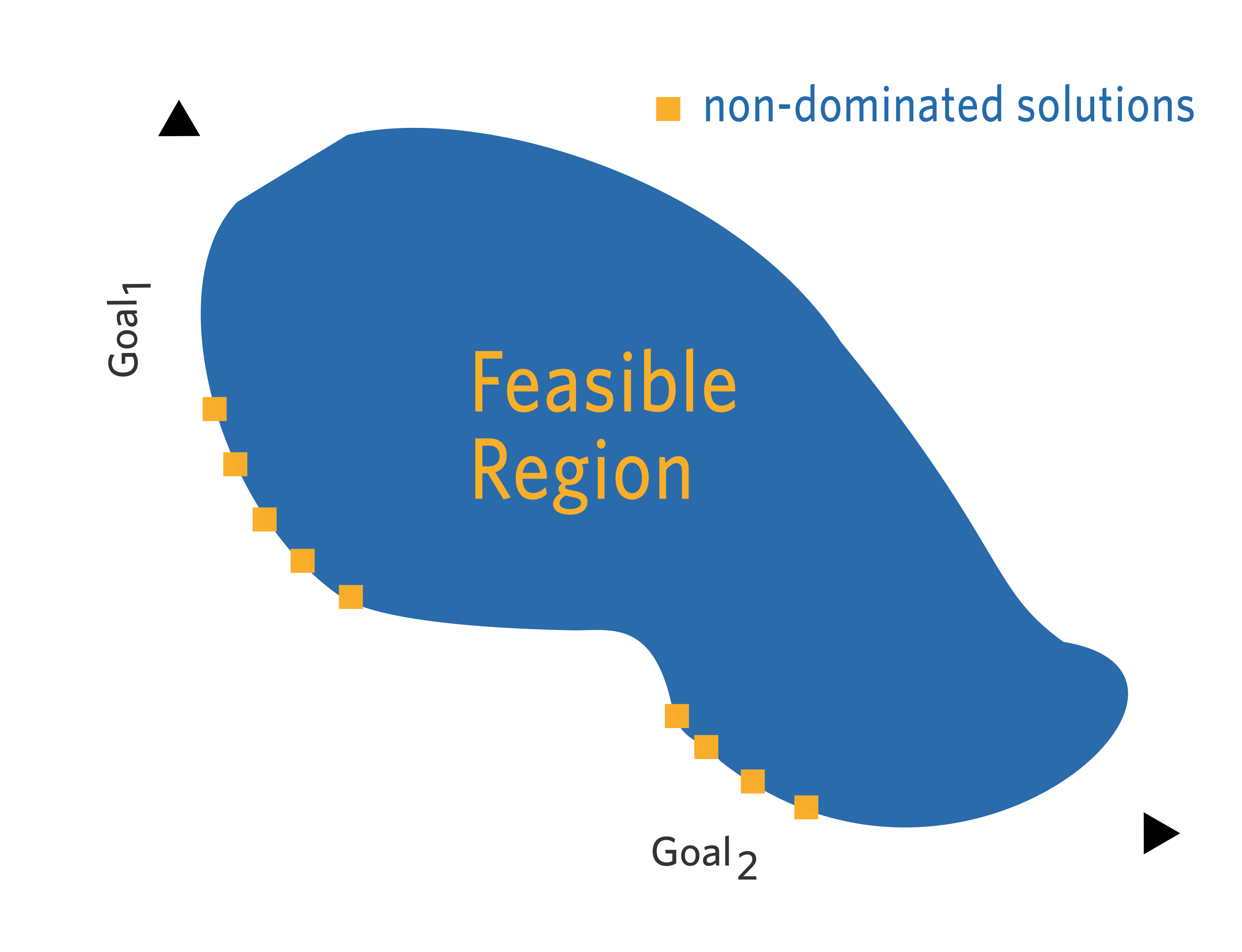
Here S is the D-dimensional solution space and R M is the M-dimensional objective space. In general the goal of MOPs is to find a set of non-dominated solutions that approximates the Pareto front in the objective space. The main objective of a multi-objective optimization algorithm is to find this set.
Another common term and set in multi-objective optimization is Pareto optimal front. This set includes the projection of Pareto optimal solutions in the objective space. This is illustrated in Fig.
1 for a minimization problem. This figure also shows a dominated and a non-dominated solution in both parameter and. Same time the portfolio optimization problem can be treated as a multi-objective optimization problem Model 5.
One can attain Pareto optimality in this case because the formulation of Model 5 belongs to the category of convex vector optimization which guarantees that any local optimum is a global optimum 5. It is an area of multiple-criteria decision making concerning mathematical optimization problems involving more than one objective function to be optimised simultaneously. It is mainly used in places when we have objectives that are conflicting with each other and the optimal decision lies in between their trade-offs.
For the multi-objective optimization problem is it possible to apply the concept of SN ratio to individual outputs obtained through RSM or full factorial design of experiment. Multiobjective optimization MOO problem Multiple objective functions number denoted by k k 1 special case. Two objectives Objective vectors can be visualized when k 2 3 Variables.
Values change the solution Constraints. Same as in single objective problems Feasible region S. Consists of all the points satisfying the constraints.
Multiple Objective Optimization In MOO we usually want to either minimize or maximize multiple functions simultaneously. However these functions are often in conflict with one another. An improved solution for one function often means a worse solution for another function.
In contrast to single-objective optimization problems which admit at most one optimal value multi-objective optimization problems often admit several optimal points ie. Points of ZX that cannot be outperformed by another point of ZX. These points are called non-dominated points.
Multiple-Objective Optimization The set of all efficient points to a multiple - objective optimization problem is known as the efficient frontier. Regardless of how we prioritize the importance of each objective function the best solution should be selected from the efficient frontier. This is an introductory course to multi-objective optimization using Artificial Intelligence search algorithms.
We start with the details and mathematical models of problems with multiple objectives. Then we focus on understanding the most fundamental concepts in the field of multi-objective optimization including but not limited to. In this post I want to show an alternative approach for solving below multi-objective linear optimization problem.
I will use approach 1 but apply weights instead. The approach I now use is to solve the problem in two steps where a sub-problem with one objective only is solved first and its optimal outcome is added to a second sub-problem with only the the second objective as a constraint. Multiobjective Optimization Solve multiobjective optimization problems in serial or parallel Solve problems that have multiple objectives by the goal attainment method.
For this method you choose a goal for each objective and the solver attempts to find a point that satisfies all goals simultaneously or has relatively equal dissatisfaction. Intuitionistic fuzzy TOPSIS approach is a new and powerful method to solve multi-objective optimization problem and it provides better Pareto-optimal solution. It is available in the following.
In this video Im going to show you a simple but effective way to solve various multi-objective optimization problems. This approach is very easy to impleme.