Odds ratio multiple logistic regression

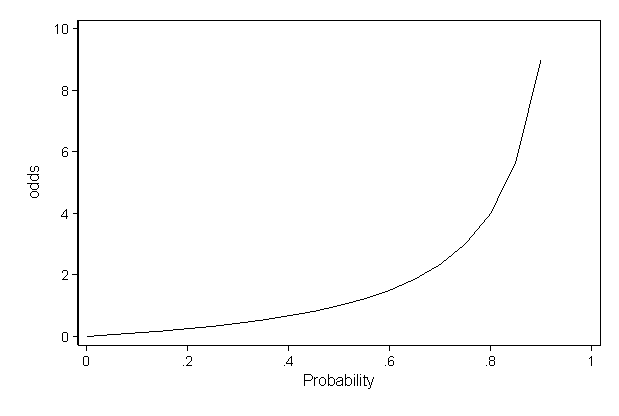
To convert logits to probabilities you can use the function exp logit 1exp logit. In words logistic regression models log odds as a linear function of the predictors.

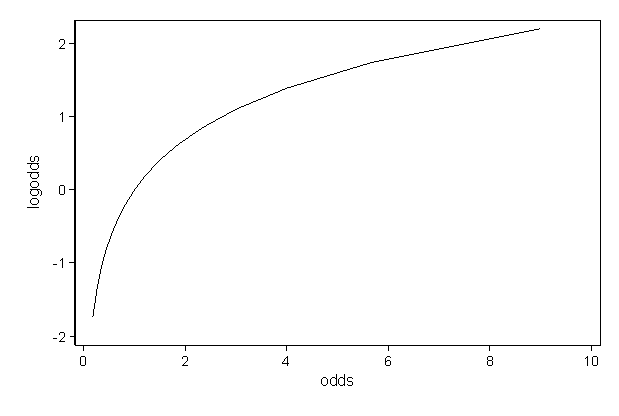
The logistic regression coefficient indicates how the LOG of the odds ratio changes with a 1-unit change in the explanatory variable.

Odds ratio multiple logistic regression. In general we can have multiple predictor variables in a logistic regression model. Logitp logp1-p β 0 β 1 x1. β k xk Applying such a model to our example dataset each estimated coefficient is the expected change in the log odds of being in an honors class for a unit increase in the corresponding predictor variable holding the other predictor variables constant at certain value.

Odds π1-π p proportional response ie. R out of n responded so π rn Logit log odds logπ1-π When a logistic regression model has been fitted estimates of π are marked with a hat symbol above the Greek letter pi to denote that the proportion is. If we define p as the probability that the outcome is 1 the multiple logistic regression model can be written as follows.

Is the expected probability that the outcome is present. X 1 through X p are distinct independent variables. And b 0 through b p are the regression coefficients.

The multiple logistic regression model is sometimes written differently. P 655 1655 868. These probabilities odds and odds ratios - derived from the logistic regression model - are identical to those calculated directly from Figure 421.

This is because we have just one explanatory variable gender and it has only two levels girls and boys. P x 1 p x e β 0 β 1 x. In words logistic regression models log odds as a linear function of the predictors.

The odds are the exponentiation of this linear combination. In the multivariate case this gives. P x 1 p x e β 0 β 1 x 1.

β n x n. Look at it as a product. Interpreting Odds Ratios An important property of odds ratios is that they are constant.

It does not matter what values the other independent variables take on. For instance say you estimate the following logistic regression model. -1370837 1685 x 1 0039 x 2 The effect of the odds of a 1-unit increase in x 1 is exp1685 118.

The logistic regression coefficient indicates how the LOG of the odds ratio changes with a 1-unit change in the explanatory variable. This is not the same as the change in the unlogged odds ratio though the 2 are close when the coefficient is. The R-code above demonstrates that the exponetiated beta coefficient of a logistic regression is the same as the odds ratio and thus can be interpreted as the change of the odds ratio when we increase the predictor variable x x by one unit.

In this example the odds ratio is 268. The coefficient returned by a logistic regression in r is a logit or the log of the odds. To convert logits to odds ratio you can exponentiate it as youve done above.

To convert logits to probabilities you can use the function exp logit 1exp logit. However there are some things to note about this procedure. In logistic regression however the regression coefficients represent the change in the logit for each unit change in the predictor.

Given that the logit is not intuitive researchers are likely to focus on a predictors effect on the exponential function of the regression coefficient the odds ratio. Logistic regression Number of obs 11673 LR chi210 67286 Prob chi2 00000 Log likelihood -33554983 Pseudo R2 00911 mortality Odds Ratio Std. Z Pz 95 Conf.

Interval Gender Female 3306906 1418547 279 0005 1426547 7665802 age_10 1591416 0581228 1272 0000 1481479 1709511 AMI_type. Now however the B coefficient for remploy 1 is 0087 meaning that in this multiple logistic regression that controls for education level the odds of an employed person being unaware of neighbourhood policing are now higher than those of an economically inactive person. Odds Ratio Probability of stayingProbability of exit.

The formula for calculating probabilities out of odds ratio is as follows P stay in the agricultural sector OR1OR. Find the adjusted odds ratio of CVD for diabetics compared to non-diabetics. From the multiple logistic regression analysis we found that the odds ratio was 363 adjusting for age and sex.

Calculate the percentage change in the odds ratio and determine whether confounding is present. This video shows how to perform a Logistic Regression to find an odds ratio in the Visual Dashboard of Epi Info 7. Confidence Intervals for the Odds Ratio in Logistic Regression with One Binary X 864-2 NCSS LLC.

These values are combined in the odds ratio OR of P 1 to P 0 resulting in 𝑂𝑂𝑅𝑅𝑦𝑦𝑦𝑦 exp𝛽𝛽1 or by taking the logarithm of both sides simply log 𝑂𝑂𝑅𝑅𝑦𝑦𝑦𝑦 log 𝑃𝑃1.