R γ D θ. This thesis presents research on the force and deflection behavior of beams with rectangular crosssections undergoing lateral torsional buckling.

If it is not possible to avoid subjecting a member to significant torsional moment.
Torsional deflection of a beam. The equation for the torsion of a beam in the elastic range is analogous to that for small deflections of a membrane under uniform pressure. Figure 1-66 shows such a membrane. The pressure on the membrane is designated as p and S is the uniform tension per unit at its boundary.
Lateral Torsional Buckling in Beams Lateral Deflection Torsion Summary Lateral torsional buckling occurs when an applied load causes both lateral displacement and twisting of a member. This failure is usually seen when a load is applied to an unconstrained steel I-beam with the two flanges acting differently one under compression and the other tension. What is torsion.
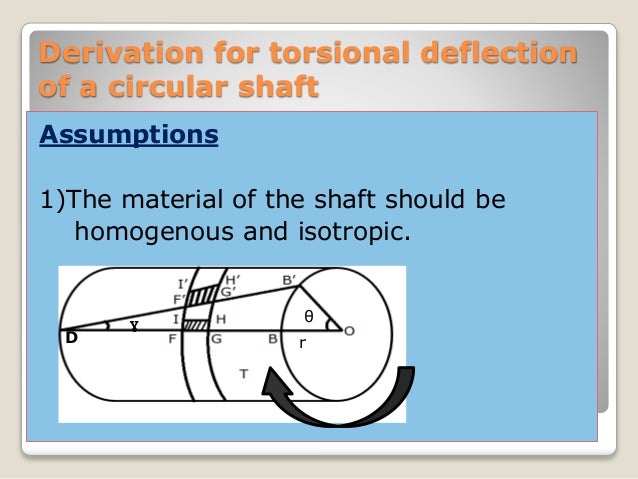
Torsion is the twisting of an object due to an applied torque. Torsional deflection is the angular displacement or deformation of a body when a twisting force is applied. Derivation for torsional deflection of a circular shaft Assumptions 1The material of the shaft should be homogenous and isotropic.
R γ D θ. Beam Torsional Deflection Formula. October 14 2019 - by Arfan - Leave a Comment.
Shaft with torsional and bending tlp library bending and torsion of beams uniformly distributed torsion in hss what is the displacement of a bent beam ysis of deep beams with torsion. Take all reasonable steps to eliminate torsional effects avoiding eccentricity by placing beams in line with the loads or adding beams in another direction to carry the eccentric loads in direct bending. If it is not possible to avoid subjecting a member to significant torsional moment.
When the beam is cut at the section either side of the beam can be considered when solving for the reactions. The side that is selected does not affect the results so choose whichever side is easiest. In the figure above the side of the beam to the right of the section cut was selected.
The reactions at the section cut are shown with blue arrows. The lateral torsional buckling is the deformation of the beam due to the applied loads away from its longitudinal axis. Further it causes steel beams failures.
The deformation could occur as translational and rotational movement of the section and these types of movements are identified as lateral torsional buckling. Where pb bending strength allowing for susceptibility to lateral -torsional buckling. Zp plastic section modulus.
It should be noted that pb fy for low values of slenderness of beams and the value of pb drops as the beam becomes longer and the beam slenderness calculated as given below increases. This behaviour is analogous to columns. A bar of uniform section fixed at one end and subject to a torque at the extreme end which is applied normalto its axis will twist to some angle which is proportional to the applied torque.
This assumes that the bar is not stressedto a level greater than its elastic limit. Torsional deflection of shaft negative bending moment quora shear force bending moment structural ering structural ering10 Simply Supported Beam Under Concentrated Load At Mid Span And Scientific DiagramTorsionBuilt In Beams Materials Ering. Is the beam length part of the formula for torsional deflection of a rectangular beam as it is with a round beam ie torsional deflection angle for round beam TLJG in radians.
Where T Torque in-lb L Length in inches J Polar moment of inertia G Modulus of rigidity. Angular Deflection of Solid Cylinder or Shaft with Torsion Applied. The angular deflection of a solid cylinder with torsion loading applied.
θ L T G J Open Torsional Deflection of Shaft Calculator. θ angular shaft deflection radians T torque N-mm in-lb L length of shaft mm in. This thesis presents research on the force and deflection behavior of beams with rectangular crosssections undergoing lateral torsional buckling.
The large 3D deflection path of buckling beam tips was closely approximated by circular arcs in two planes. The beam will be subjected to stresses due to torsion as well as due to bending. The effect of torsional loading can be further split into two parts the first part causing twist and the second warping.
These are discussed in detail in the next section. In 1820 the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the second moment of area normal to the section J zz which has an exact analytic equation by assuming that a plane section before twisting remains planar after twisting and a diameter remains a straight line.
Unfortunately that assumption is correct only in beams with circular cross-sections. Describes the deflection of the beam in the direction at some position recall that the beam is modeled as a one-dimensional object. Is a distributed load in other words a force per unit length analogous to pressure being a force per area.
It may be a function of. Inadequate beam stiffness can lead to large deflections and may also cause high localised stresses and a danger of failure in that region. In addition to bending moments such structures may be subjected to twisting or torsional moments torques.
Builders use hollow rectangular beams in construction because such beams can withstand the forces of shearing and bending in both the x- and y-directions. They are also resistant to torsional forces much more so than I-beams. This online Mechanical Engineering Calculator is to compute the deflection of hollow rectangular beams.